Siły w ruchu harmonicznymkurs
Siły w ruchu harmonicznym
Ruch harmoniczny mogą powodować różne siły. Muszą one jednak spełniać jeden podstawowy warunek: siła musi być proporcjonalna do wychylenia ciała z punktu równowagi i skierowana przeciwnie do tego wychylenia. Skąd to wiem? Wiemy już, że
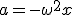 . Skoro przyspieszenie jest proporcjonalne od wychylenia i skierowane przeciwnie, to siła również. Najbardziej znaną siłą o takich właściwościach jest siła sprężystości. Rzeczywiście, prawo Hooke’a zapewnia tę proporcjonalność, a i współczynnik proporcjonalności jest ujemny, bo siła sprężystości jest skierowana przeciwnie do wychylenia ciała z położenia równowagi.
. Skoro przyspieszenie jest proporcjonalne od wychylenia i skierowane przeciwnie, to siła również. Najbardziej znaną siłą o takich właściwościach jest siła sprężystości. Rzeczywiście, prawo Hooke’a zapewnia tę proporcjonalność, a i współczynnik proporcjonalności jest ujemny, bo siła sprężystości jest skierowana przeciwnie do wychylenia ciała z położenia równowagi.Dalsza część kursu dostępna
dla użytkowników  premium
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.