Średnia arytmetyczna, geometryczna i harmonicznakurs
Definicja
1) Średnia arytmetyczna dwóch liczb
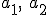 .
.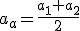
2) Średnia geometryczna liczb nieujemnych.
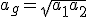
3) Średnia harmoniczna
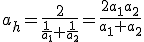
Ogólnie:
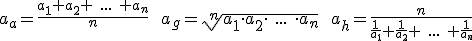
Prawdziwe jest …
Twierdzenie
Dla dodatnich
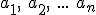 zachodzi:
zachodzi: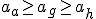
Ogólny dowód jest trudny.
Łatwo dowodzi się tego twierdzenia dla dwóch liczb.
Liczby
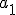 i
i 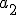 są dodatnie, więc istnieją pierwiastki z tych liczb. Utwórzmy różnicę tych pierwiastków.
są dodatnie, więc istnieją pierwiastki z tych liczb. Utwórzmy różnicę tych pierwiastków.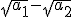
Znak tej różnicy jest oczywiście dowolny, ale jak podniesiemy ją do kwadratu to już musi być nieujemna.
^2 \ge 0)
Skorzystajmy ze wzoru skróconego mnożenia.
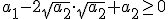
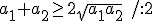
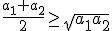
Zatem
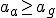
Jeśli same te liczby odejmiemy i różnicę podniesiemy do kwadratu, otrzymamy liczbę nieujemną.
^2 \ge 0<br>)
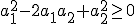
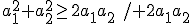
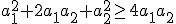
^2 \ge 4a_1a_2\ /\cdot a_1a_2<br>)
^2 \ge 4a_1^2a_2^2\ /:(a_1 + a_2)^2<br>)
^2}<br>)
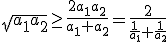
Dalsza część kursu dostępna
dla użytkowników  premium
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.