Energia w polu elektrycznym. 3.16 zadanie
zadanie
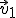 i
i 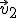 leżą w jednej płaszczyźnie i tworzą kąty
leżą w jednej płaszczyźnie i tworzą kąty 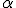 z odcinkiem je łączącym. Odległość między elektronami w chwili początkowej jest równa
z odcinkiem je łączącym. Odległość między elektronami w chwili początkowej jest równa  . Na jaką minimalną odległość zbliżą się elektrony, jeśli prędkości
. Na jaką minimalną odległość zbliżą się elektrony, jeśli prędkości 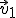 i
i 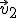 są równe co do wartości wynoszącej
są równe co do wartości wynoszącej  . Ładunek elektronu wynosi
. Ładunek elektronu wynosi  , a masa
, a masa 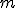 .
.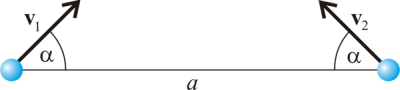
Rozwiązanie zadania dostępne
dla użytkowników  premium
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.